Area of Trapezium: समलम्ब एक चौड़ी आकृति होती है। समलम्ब के क्षेत्रफल की गणना करने के लिए विभिन्न सूत्रों का प्रयोग किया जाता है। इस लेख में, हम समलम्ब के क्षेत्रफल को निर्धारित करने के विभिन्न तरीकों पर विचार करेंगे और इसके महत्व को समझेंगे।
समलम्ब क्या होता है?
समलम्ब एक चार भुजाओं वाली आकृति है जिसमें समांतर भुजाओं का एक सेट होता है। समांतर भुजाओं को समलम्ब चतुर्भुज का आधार कहा जाता है, और असमांतर भुजाओं को पाद कहा जाता है। एक समलम्ब चतुर्भुज की ऊंचाई आधारों के बीच की लंबवत दूरी होती है। एक समलम्ब चतुर्भुज का क्षेत्रफल आधारों के औसत को ऊंचाई के गुणनफल के बराबर होता है।
समलम्ब प्रकृति और रोजमर्रा की जिंदगी में एक सामान्य आकार है। उदाहरण के लिए, तितली के पंख, घर की छत और आरी के दाँत सभी समलम्ब चतुर्भुज हैं। समलम्ब का उपयोग कई अलग-अलग संरचनाओं और मशीनों, जैसे पुल, हवाई जहाज और कारों में भी किया जाता है।
समलम्ब चतुर्भुज का क्षेत्रफल : परिभाषा
एक समलंब एक 2D आकृति है, यह एक चतुर्भुज है और इसकी 4 भुजाएँ हैं जिनमें से 2 भुजाएँ एक-दूसरे के समांतर होती हैं। एक समलम्ब चतुर्भुज का क्षेत्रफल दो त्रिभुजों के क्षेत्रफलों और आयत के क्षेत्रफल के योगफल के बराबर होता है। एक समलंब जिसकी दो समांतर भुजाएँ समान होती हैं और एक आधार पर समान कोण बनाती हैं, समद्विबाहु समलंब कहलाता है।
समलंब के प्रकार
समलंब को नीचे बताए अनुसार 3 विशिष्ट वर्गों में विभाजित किया गया है:
- आइसोसेलियस ट्रेपेज़ियम: इसे एक समलंब के रूप में परिभाषित किया जा सकता है जिसमें दोनों पाद और आधार कोण समान माप के होते हैं।
- राइट ट्रेपेज़ियम: एक राइट ट्रेपेज़ियम दो समकोण वाला समलंब होता है।
- स्केलीन ट्रेपेज़ियम: एक स्केलीन ट्रेपेज़ियम एक ट्रेपेज़ियम है जिसकी कोई भी भुजा समान माप की नहीं होती है।
समलम्ब चतुर्भुज का क्षेत्रफल : विशेषताएँ
समांतर भुजाओं के कम से कम एक युग्म वाले चतुर्भुज को अमेरिकी और कनाडाई अंग्रेजी में ट्रैपेज़ॉइड कहा जाता है। ब्रिटिश और अंग्रेजी के अन्य रूपों में, ट्रैपेज़ॉइड को ट्रैपेज़ियम कहा जाता है। ट्रैपेज़ियम या समलंब एक चतुर्भुज है जिसमें विपरीत भुजाओं का एक युग्म एक-दूसरे के समांतर होता है और समलंब का दूसरा युग्म समांतर नहीं होता है। एक समलंब के कुछ गुण नीचे सूचीबद्ध हैं:
- एक समलंब के कोणों का योगफल 360º होता है।
- एक समलंब एक समांतर चतुर्भुज नहीं है (क्योंकि एक समलंब में विपरीत भुजाओं का केवल एक युग्म समांतर होता है और हमें समांतर चतुर्भुज में दोनों भुजाओं के युग्म समांतर होने चाहिए)।
- एक समलंब चतुर्भुज की 4 भुजाएँ असमान होती हैं जब तक कि यह एक समद्विबाहु समलंब न हो जिसमें 2 समांतर भुजाएँ बराबर हों।
- समलंब के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
- एक समलंब के आसन्न कोणों के दो युग्मों का योगफल 180º तक होता है।
समलम्ब चतुर्भुज का परिमाप
समलम्ब चतुर्भुज की परिधि समलम्ब चतुर्भुज या समलम्ब चतुर्भुज की भुजाओं द्वारा निर्मित सीमा की लंबाई का कुल योग है। यह एक तिरछा बहुभुज है। चूँकि सभी रेखाएँ और कोने द्विविमीय समतल में समाहित हैं, इसलिए समलम्ब चतुर्भुज की परिधि द्विविमीय आकार में समाहित है।
मान लीजिए कि हमारे पास एक समलम्ब चतुर्भुज ABCD है जिसकी भुजाएँ AB और CD एक दूसरे के समांतर हैं। जबकि AD और BC गैर-समांतर भुजाएँ हैं, वे जोड़ी के ‘आधार’ बनाती हैं (अर्थात, वे पैर हैं)। मान लीजिए कि समलम्ब चतुर्भुज की परिधि “P” इकाइयों के समान है।
समलम्ब चतुर्भुज ABCD की परिधि इस प्रकार दी गई है,
P = AB + BC + CD + AD.
क्षेत्रफल के संदर्भ में समलम्ब चतुर्भुज की परिधि निम्न सूत्र द्वारा दी गई है,
P = गैर-समांतर भुजाओं की लंबाई का योग + 2(A/h)
जहाँ A समलम्ब चतुर्भुज का क्षेत्रफल है और h इसकी ऊँचाई है।
समलम्ब चतुर्भुज के क्षेत्रफल का सूत्र
समलंब के क्षेत्रफल की गणना करने के लिए, आपको दो समांतर रेखाओं के बीच एक लंब खींचने की आवश्यकता है। लंब को ऊँचाई को ‘h’ के रूप में निरूपित किया जाएगा जो समांतर भुजाओं के बीच की दूरी है।
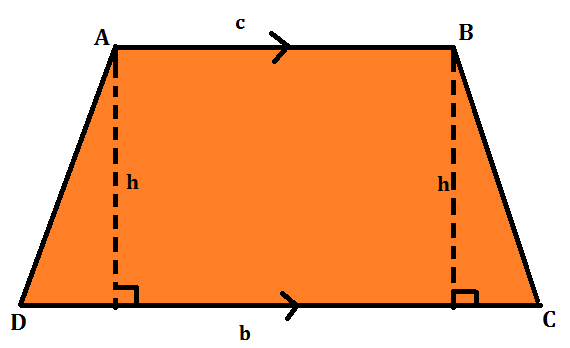
इसलिए, एक समलंब का क्षेत्रफल नीचे दिए गये सूत्र से निकाला जा सकता है:
समलंब चतुर्भुज का क्षेत्रफल = 1/2 x समांतर भुजाओं के बीच की दूरी x समांतर भुजाओं का योगफल
क्षेत्रफल = 1/2 x h x (AB + DC)
समलम्ब चतुर्भुज के क्षेत्रफल पर आधारित प्रश्न
उदहारण 1: एक समलंब की दो समांतर भुजाओं की लंबाई 3: 2 के अनुपात में दी गई है और उनके बीच की दूरी 8 सेमी है। यदि समलंब का क्षेत्रफल 400 वर्ग सेमी है, तो समांतर भुजाओं की लंबाई ज्ञात करें।
हल: माना कि, 2 समांतर भुजा 3x और 2x दी गई हैं।
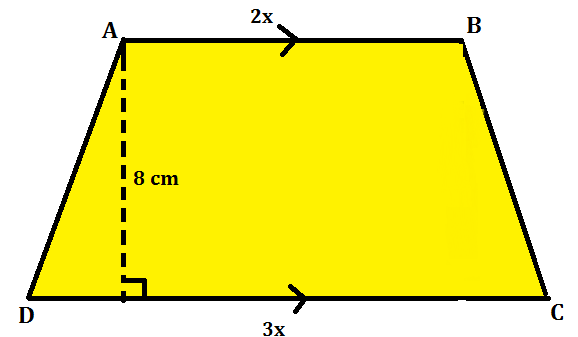तो समलंब का क्षेत्रफल = 1/2 x समांतर भुजाओं के बीच की दूरी x समांतर भुजाओं का योगफल
400= 1/2 x (3x + 2x) x 8
400 = 1/2 x 5x x 8
400 = 20x => x = 20 सेमी
समांतर भुजाओं की लंबाई 60 सेमी और 40 सेमी है।
हल:
समलंब का क्षेत्रफल = 1/2 x समांतर भुजाओं के बीच की दूरी x समांतर भुजाओं का योगफल
समलंब का क्षेत्रफल = {¹/₂ × (27 + 19) × 14} cm² = 322 सेमी²
Q3. एक समलंब का क्षेत्रफल 352 सेमी² है और इसकी समांतर भुजाओं के बीच की दूरी 16 सेमी है। यदि समांतर भुजा में से एक की लंबाई 25 सेमी है, तो दूसरी भुजा की लंबाई ज्ञात करें।
हल:
मान लीजिए अभीष्ट भुजा की लंबाई x सेमी है।
तो समलंब का क्षेत्रफल= {¹/₂ × (25 + x) × 16} सेमी²
समलंब का क्षेत्रफल = (200 + 8x) सेमी².
लेकिन समलंब का क्षेत्रफल = 352 सेमी² (दिया गया है)
अतः, 200 + 8x = 352
⇒ 8x = (352 – 200)
⇒ 8x = 152
⇒ x = (152/8)
⇒ x = 19.
दूसरे भुजा की लंबाई 19 सेमी है।
Q4. एक समलंब का क्षेत्रफल क्या है जब आधार क्रमशः 12 सेमी और 20 सेमी हैं और दो समानांतर भुजाओं के बीच की दूरी 10 सेमी है?
हल: दिया गया है,
a = 12 सेमी
b = 20 सेमी
दो समान्तर भुजाओं के बीच की दूरी, h = 10 सेमी
समलम्ब चतुर्भुज का क्षेत्रफल = 1/2 (12 + 20) 10
= 160 सेमी²
त्रिकोणमितिः सूत्र, टिप्स, सर्वसमिकाएँ औ...
मिश्रण और सम्मिश्रण, नोट्स, तरीके और प्र...
आवर्त सारणी: तत्व, समूह, विशेषता और इसके...
