मात्रक और मापन एक महत्वपूर्ण वैज्ञानिक और गणितीय अवधारणा है, जो हर क्षेत्र में उपयोगी होती है। मात्रक और मापन का अध्ययन न केवल विज्ञान, गणित, और इंजीनियरिंग में महत्वपूर्ण है, बल्कि यह भौतिकी, रसायन विज्ञान, और अन्य क्षेत्रों में भी महत्वपूर्ण योगदान करती है। मात्रक और मापन की अच्छी समझ से हम दुनिया के प्राकृतिक विभाजन, उसके अनुसंधान, और वैज्ञानिक अध्ययन में मदद कर सकते हैं। इसलिए, यह एक अहम विषय है जो हर विद्यार्थी को समझना चाहिए।
मात्रक और मापन
समय, द्रव्यमान और लंबाई जैसी भौतिक राशियों की गणना करने के लिए, हमें मापन के कुछ मानकों की आवश्यकता होती है। मापन के इन मानकों को भौतिक राशियों के मात्रक कहा जाता है। इस लेख में, हम मात्रक और मापन के बारे में विस्तृत जानकारी प्रदान करेंगे।
हमें मानक मात्रकों और मापों की आवश्यकता क्यों होती है?
क्षेत्रफल, द्रव्यमान, लंबाई, आयतन आदि जैसी विभिन्न मात्राओं की गणना के लिए कई पद्धतियाँ और मात्रक मौजूद हैं। उदाहरण के लिए,
- एक एकड़ भारत में आकार मापने का एक पारंपरिक तरीका है। मीट्रिक प्रणाली के अनुसार एक एकड़ 4046 वर्ग मीटर के बराबर है।
- तापमान की गणना डिग्री सेल्सियस में की जाती है, लेकिन एक छड़ की लंबाई को उसी इकाई में नहीं मापा जा सकता है।
तो, अब अनुमान लगाया जा सकता है कि बिना मानक शब्दों की राशियों को मापना कितना कठिन होगा। प्रत्येक राशि को अपने तरीके से मापा जाना चाहिए। परिमाण और माप राशि के साथ-साथ भिन्न-भिन्न होते हैं। इसलिए प्रत्येक राशि के लिए माप के मात्रकों की आवश्यकता उत्पन्न होती है।
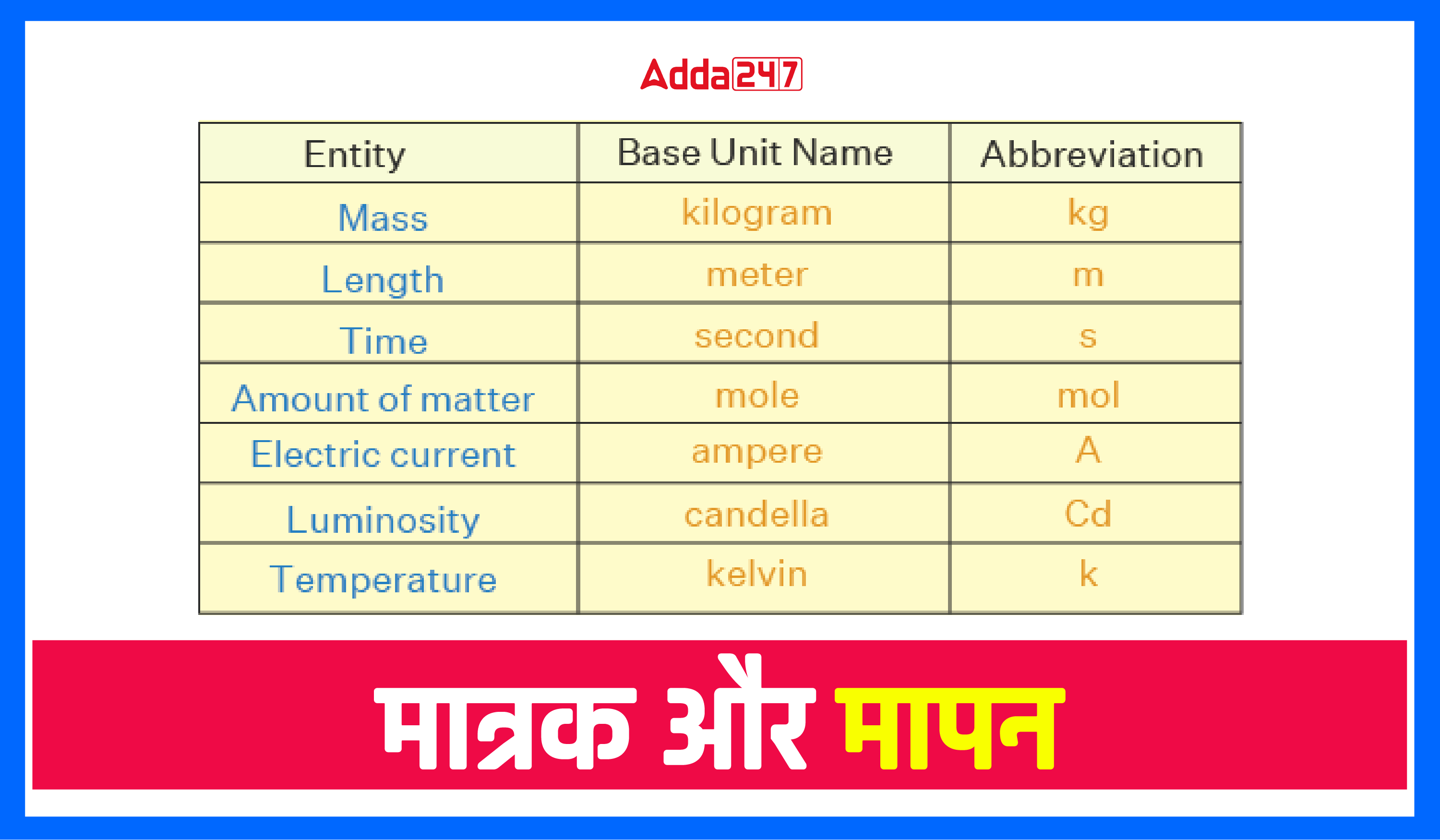
मूल भौतिक राशियाँ/मात्रक
वे राशियाँ जो भौतिकी के नियमों का वर्णन कर सकती हैं, भौतिक राशियाँ कहलाती हैं। भौतिक राशि वह है जिसे मापा जा सकता है। इस प्रकार, लंबाई, द्रव्यमान, समय, दबाव, तापमान, धारा और प्रतिरोध को भौतिक राशियाँ माना जाता है। राशियों के मात्रकों को मूल मात्रक कहा जाता है। भौतिक राशियों को दो भागों में वर्गीकृत किया गया है
मूल राशियाँ या आधार राशियाँ
वे भौतिक राशियाँ जो एक दूसरे से स्वतंत्र होती हैं, मूल राशियाँ कहलाती हैं।
| मूल राशियाँ और मात्रक | |||
| राशि | मात्रक | प्रतीक | परिभाषा |
| लंबाई | मीटर | m | एक मीटर (1/299792458) सेकंड के समय अंतराल के दौरान निर्वात में प्रकाश द्वारा तय की गई दूरी है। |
| द्रव्यमान | किलोग्राम | kg | यह पेरिस के नेशनल ब्यूरो ऑफ वेट एंड मेजरमेंट्स में रखे गए प्लैटिनम-इरिडियम बेलन का द्रव्यमान है। |
| समय | सेकंड | s | सेकंड सीज़ियम-133 परमाणु द्वारा उत्सर्जित एक निर्दिष्ट तरंग दैर्ध्य के प्रकाश द्वारा 9192631770 कंपन करने में लिया गया समय है। |
| विद्युत धारा | ऐमपीयर | A | एक ऐम्पीयर वह धारा है, जो निर्वात में 1 मीटर की दूरी पर रखे गए अनंत लंबाई और नगण्य अनुप्रस्थ-काट के क्षेत्रफल वाले दो सीधे समांतर चालकों के माध्यम से प्रवाहित होने पर उनके बीच 2 x 10-7 न्यूटन प्रति मीटर लंबाई के बराबर बल उत्पन्न करती है। |
| तापमान | केल्विन | K | यह जल के त्रिक बिंदु के ऊष्मागतिक तापमान का 1/273.6 भाग होता है। |
| पदार्थ की मात्रा | मोल | mol | एक मोल पदार्थ की वह मात्रा है जिसमें 0.012 किलोग्राम कार्बन-12 में परमाणुओं की संख्या के बराबर प्राथमिक मात्रक होते हैं। |
| ज्योति तीव्रता | कैडेला | cd | एक कैंडेला को प्लैटिनम (1773 0C) के हिमांक तापमान पर रखे एक आदर्श कृष्ण पिंड के 1 वर्ग सेंटीमीटर की ज्योति तीव्रता के 1/60वें हिस्से के रूप में परिभाषित किया गया है। |
इन सात राशियों के अतिरिक्त दो पूरक राशियाँ भी होती हैं।
| पूरक राशियाँ और मात्रक | |||
| राशि | मात्रक | प्रतीक | परिभाषा |
| समतल कोण | रेडियन | rad | रेडियन वृत्त के केंद्र पर चाप द्वारा बनाया गया कोण है जिसकी लंबाई वृत्त की त्रिज्या के बराबर होती है। |
| ठोस कोण | स्टेरेडियन | sr | स्टेरेडियन किसी गोले के केंद्र पर उसकी त्रिज्या के वर्ग के बराबर क्षेत्रफल की गोलाकार सतह द्वारा बनाया गया ठोस कोण है। |
व्युत्पन्न राशियाँ
अन्य सभी राशियाँ जिन्हें मूल राशियों के रूप में व्यक्त किया जा सकता है, व्युत्पन्न राशियाँ कहलाती हैं।
| व्युत्पन्न राशियाँ और मात्रक | |
| राशि | मात्रक |
| विस्थापन | m |
| क्षेत्रफल | m2 |
| आयतन | m3 |
| वेग | ms-1 |
| त्वरण | ms-2 |
| घनत्व | Kg m-3 |
| संवेग | Kg ms-1 |
| कार्य/ऊर्जा/ऊष्मा | जूल (या) Kg m2/sec2 |
| शक्ति | वाॅट(W) (या) जूल/sec |
| कोणीय वेग | rad s-1 |
| कोणीय त्वरण | rad s-2 |
| जड़त्व आघूर्ण | Kg m2 |
| बल | न्यूटन (या) Kg m/sec2 |
| दाब | न्यूटन/m (या) Kg m-1/sec2 |
| आवेग | न्यूटन sec (या) Kg m/sec |
| जड़त्व | Kg m2 |
| विद्युत धारा | ऐम्पीयर (या) C/sec |
| प्रतिरोध/प्रतिबाधा | ओम (या) Kg m2/sec C2 |
| EMF/वोल्टता/विभव | वोल्ट (या) Kg m2/sec2 C |
| चुंबकशीलता | हेनरी/m (या) Kg m/C2 |
| वैद्युतशीलता | फैराडे/m (या) sec2C2/Kgm3 |
| आवृत्ति | हर्ट्ज़ (या) sec-1 |
| तरंगदैर्ध्य | m |
मात्रकों की पद्धति
- FPS पद्धति: इस पद्धति में लंबाई की इकाई फुट, द्रव्यमान के मात्रक पाउंड और समय की इकाई सेकंड है।
- CGS पद्धति: इस पद्धति में लंबाई, द्रव्यमान और समय के मात्रक क्रमशः सेंटीमीटर, ग्राम और सेकंड हैं।
- MKS पद्धति: इस पद्धति में लंबाई, द्रव्यमान और समय के मात्रक क्रमशः मीटर, किलोग्राम और सेकंड होती है।
- SI पद्धति: यह पद्धति दुनिया भर में सभी मापों में व्यापक रूप से उपयोग की जाती है। यह पद्धति सात मूल मात्रकों और दो पूरक मात्रकों पर आधारित है।
SI मात्रक प्रीफिक्स
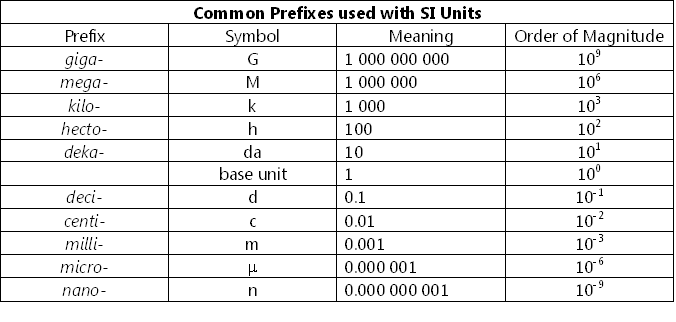
SI पद्धति मूल मात्रकों के लिए प्रीफिक्स की एक मानक पद्धति का उपयोग करती है, जिससे उन्हें सापेक्ष परिमाण में अधिक प्रासंगिक और वर्णनात्मक बनाया जा सकता है। प्रीफिक्स का उपयोग मूल मात्रक के गुणजों या भिन्नों की पहचान करने के लिए किया जाता है। नीचे दी गई तालिका मापन के SI मात्रकों के लिए मानक प्रीफिक्स को सूचीबद्ध करती है।
विमाएँ और विमीय सूत्र
किसी भौतिक राशि की विमा वे घातें (या घातांक) हैं जिनसे उस राशि का प्रतिनिधित्व करने के लिए आधार राशियों पर घात लगाकर उस भौतिक राशि को दर्शाया जाता है। विमीय समीकरण वे समीकरण हैं, जो किसी भौतिक राशि की विमाओं को आधार राशियों के रूप में दर्शाते हैं।
उदाहरण के लिए,
- आयतन का विमीय सूत्र, [V] = [M0L1T-1]
- चाल का विमीय सूत्र, [v] = [M0LT-1]
- बल का विमीय सूत्र, [F] = [M1L1T-2]
- द्रव्यमान घनत्व, [ρ] = [ML3T0]
किसी भौतिक राशि के लिए विमीय सूत्र कैसे लिखा जाता है?
- भौतिक राशि का सूत्र अवश्य लिखना चाहिए। राशि समीकरण के बायीं ओर होनी चाहिए।
- सूत्र के दाहिनी ओर की सभी राशियाँ द्रव्यमान, लंबाई और समय जैसी मूलभूत राशियों के रूप में लिखी जानी चाहिए।
- द्रव्यमान, लम्बाई और समय को क्रमशः M, L और T से बदलें।
- पदों की घातें लिखिए।
- विमाओं की होमोजेनिटी के सिद्धांत के अनुसार, किसी दिए गए भौतिक समीकरण में सभी पद समान होने चाहिए।
उदाहरण के लिए, s = ut + (½) at2
विमाओं के अनुसार समीकरण, [L] = [LT-1.T] + [LT-2. T2]
[L] = [L] + [L]
बायाँ पक्ष = दायाँ पक्ष
विमाओं की विशेषताएँ
- विमाएँ मात्रकों की पद्धति पर निर्भर नहीं करती हैं।
- समान विमाओं वाली राशियाँ एक-दूसरे से जोड़ी या घटाई जा सकती हैं।
- विमाएँ भौतिक राशियों के मात्रकों से प्राप्त किए जा सकते हैं और इसके विपरीत भी किया जा सकता है।
- दो अलग-अलग राशियों की विमाएँ समान हो सकती हैं।
- जब दो विमाओं को गुणा या भाग किया जाता है, तो यह तीसरी राशि का विमा बनेगी।
कुछ व्युत्पन्न राशियों के मात्रक और विमाएँ
| व्युत्पन्न राशियाँ और विमाएँ |
|
| राशि | विमीय सूत्र |
| विस्थापन | M0L1T0 |
| क्षेत्रफल | M0L2T0 |
| आयतन | M0L3T0 |
| वेग | M0L1T-1 |
| त्वरण | M0L1T-2 |
| घनत्व | M1L-3T0 |
| संवेग | M1L1T-1 |
| कार्य/ऊर्जा/ऊष्मा | M1L2T-2 |
| शक्ति | M1L2T-3 |
| कोणीय वेग | M0L0T-1 |
| कोणीय त्वरण | M0L0T-2 |
| जड़त्व आघूर्ण | M1L2T0 |
| बल | M1L1T-2 |
| दाब | M1L-1T-2 |
| आवेग | M1L1T-1 |
| जड़त्व | M1L2T0 |
| विद्युत धारा | QT-1 |
| प्रतिरोध/प्रतिबाधा | ML2T-1Q-2 |
| EMF/वोल्टता/विभव | ML2T-2Q-1 |
| चुंबकशीलता | MLQ-2 |
| वैद्युतशीलता | T2Q2M-1L-3 |
| आवृत्ति | T-1 |
| तरंगदैर्ध्य | L1 |
विमीय विश्लेषण के अनुप्रयोग
- किसी भौतिक समीकरण की सत्यता की जाँच करना।
- विभिन्न भौतिक राशियों के बीच संबंध प्राप्त करना।
- किसी भौतिक राशि को मात्रकों की एक पद्धति से दूसरी पद्धति में परिवर्तित करना।


 SSC और रेलवे परीक्षाओं के लिए 'रक्त' पर ...
SSC और रेलवे परीक्षाओं के लिए 'रक्त' पर ...


