वेन आरेख, रीज़निंग, प्रतीक, आरेख और सूत्र

वेन आरेख (Venn Diagram) तर्कशास्त्र और गणित में एक महत्वपूर्ण साधन है, जिसका उपयोग विभिन्न सेटों के बीच संबंधों को दर्शाने के लिए किया जाता है। यह आरेख सामान्यतः वृत्तों या अन्य ज्यामितीय आकृतियों के रूप में प्रस्तुत किया जाता है, जहाँ प्रत्येक आकृति एक सेट का प्रतिनिधित्व करती है, और इनके बीच का ओवरलैप या इंटरसेक्शन विभिन्न सेटों के बीच के साझा तत्वों को दिखाता है। वेन आरेख का उपयोग विशेष रूप से रीज़निंग और प्रतीकात्मक तर्क में किया जाता है, जहां विभिन्न परिस्थितियों या समूहों के बीच संबंधों का विश्लेषण किया जाता है। इस लेख में, हम वेन आरेख की मूल अवधारणा, इसके प्रतीकों, विभिन्न प्रकार के आरेखों, और इससे जुड़े महत्वपूर्ण सूत्रों पर चर्चा करेंगे, साथ ही इसे हल करने के लिए कुछ ट्रिक्स और उदाहरण भी प्रदान करेंगे।

वेन आरेख क्या होते हैं?

वेन आरेख विभिन्न सेटों के बीच गणितीय या तार्किक संबंधों का एक ग्राफिकल प्रतिनिधित्व है। इसमें ओवरलैपिंग सर्कल होते हैं, जिनमें से प्रत्येक एक सेट का प्रतिनिधित्व करता है, जिसमें ओवरलैपिंग क्षेत्र सेट द्वारा साझा किए गए सामान्य तत्वों को दर्शाते हैं। वेन आरेखों का उपयोग संबंधों के दृश्य प्रतिनिधित्व के लिए किया जाता है क्योंकि वे यह दिखाने के लिए एक स्पष्ट, दृश्य विधि प्रदान करते हैं कि विभिन्न सेट कैसे प्रतिच्छेद करते हैं, ओवरलैप करते हैं, या अलग रहते हैं। यह गणित में सेटों के बीच जटिल संबंधों को समझने में मदद करता है।

वेन आरेख में सेटों को वृत्तों के रूप में दर्शाया जाता है और वृत्तों को आयत के अंदर दिखाया जाता है जो सार्वभौमिक सेट का प्रतिनिधित्व करता है। एक सार्वभौमिक सेट में सभी वृत्त होते हैं क्योंकि इसमें सभी सेटों को शामिल करने वाले सभी तत्व मौजूद होते हैं।

वेन आरेख के प्रकार

आम तौर पर, वेन आरेख तीन प्रकार के होते हैं, अर्थात् दो-तत्व वेन आरेख, तीन-तत्व वेन आरेख और चार तत्व वेन आरेख, जो दी गई स्थिति पर निर्भर करते हैं। आप लेख में दिए गए वेन आरेख प्रश्नों के माध्यम से सभी प्रकारों को समझ सकते हैं।

वेन आरेख में प्रयोग किए जाने वाले प्रतीक

वेन आरेख प्रतीकों का उपयोग दिए गए तत्वों के बीच संबंध को दर्शाने के लिए किया जाता है। उदाहरणों के साथ वेन आरेख प्रतीकों पर नीचे चर्चा की गई है।

• यूनियन (∪): यह सभी सेटों के यूनियन – यानी, X और Y सेटों के भीतर सभी तत्वों का यूनिवर्स को दर्शाता है। सेट का संघ यहाँ दिया गया है।
• उभयनिष्ठ (∩): इंटरसेक्शन चयनित सेटों या समूहों के भीतर साझा या उभयनिष्ठ सभी तत्वों का प्रतिनिधित्व करता है। यह सेट X और Y के भीतर साझा या उभयनिष्ठ तत्वों (बीच में) का प्रतिनिधित्व करता है।
• कॉम्प्लीमेंट (X^C): कॉम्प्लीमेंट वह सब कुछ दर्शाता है जो किसी विशेष सेट में प्रदर्शित नहीं होता है; इस मामले में, वह सब कुछ जो सेट X में नहीं है। X के कॉम्प्लीमेंट को दर्शाने के लिए एक समीकरण XC = U/A है, जहाँ U तत्वों के दिए गए ब्रह्मांड को दर्शाता है। नीचे दिया गया आरेख U में X के पूर्ण कॉम्प्लीमेंट को दर्शाता है।

वेन आरेख में प्रयुक्त सूत्र

वेन आरेख सूत्रों का उपयोग वेन आरेखों पर आधारित समस्याओं को आसानी से हल करने के लिए किया जाता है। 2 और 3 सेटों के लिए वेन आरेख सूत्रों पर यहाँ चर्चा की गई है।

• n ( A ∪ B) = n(A ) + n ( B ) – n ( A∩ B)
• n (A ∪ B ∪ C) = n(A ) + n ( B ) + n (C) – n ( A ∩ B) – n ( B ∩ C) – n ( C ∩ A) + n (A ∩ B ∩ C)
• और इसी प्रकार, जहाँ n(A) = सेट A में तत्वों की संख्या

सेट के लिए वेन आरेख

सेट चित्रों द्वारा दर्शाई गई वस्तुओं या तत्वों का संग्रह है। सेट के लिए वेन आरेख उदाहरणों के साथ यहाँ दिए गए हैं। विषय को विस्तार से समझने के लिए इन प्रश्नों को देखें।

वेन आरेखों पर आधारित प्रश्न

वेन आरेख प्रश्नों को आसानी से हल करने के लिए अभ्यास और तार्किक क्षमता की आवश्यकता होती है। हम यहाँ अवधारणाओं की बेहतर समझ के लिए कुछ महत्वपूर्ण वेन आरेख प्रश्नों पर चर्चा करने जा रहे हैं। इसलिए अपनी आगामी परीक्षाओं के लिए इन प्रश्नों का अभ्यास करें।

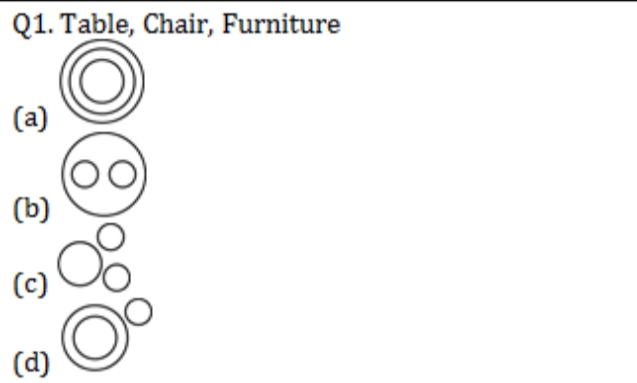
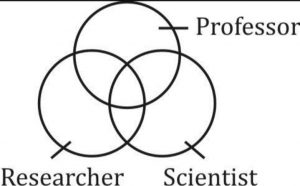
Solution: Ans (b) टेबल, कुर्सी और फर्नीचर का चित्रात्मक प्रतिनिधित्व यहां दिखाया गया है।

 

सभी समचतुर्भुज चतुर्भुज होते हैं।
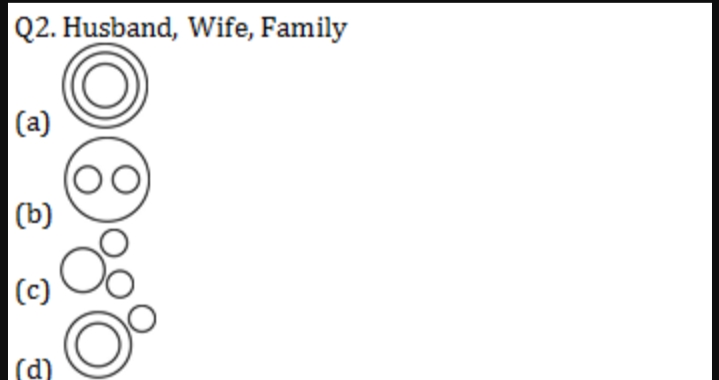
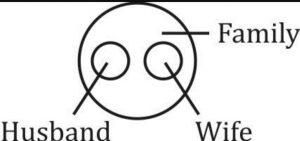
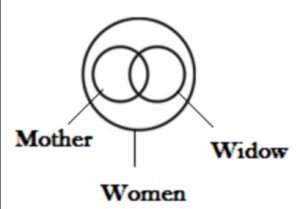
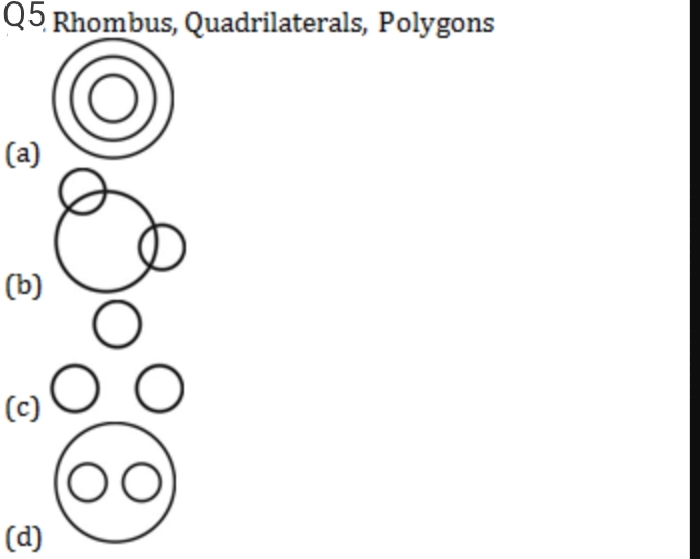
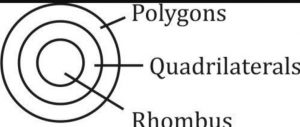
सभी चतुर्भुज बहुभुज होते हैं।

Que.6 निम्नलिखित प्रश्नों के उत्तर नीचे दिए गए आरेखों पर आधारित हैं, जहाँ त्रिभुज डॉक्टरों को दर्शाता है, वृत्त खिलाड़ियों को दर्शाता है और आयत कलाकारों को दर्शाता है।

I. आरेख में कौन सा क्रमांकित स्थान उन डॉक्टरों को दर्शाता है जो खिलाड़ी और कलाकार भी हैं?

(a) 2

(b) 3

(c) 4

(d) 5

Ans. (d)

Sol. अभीष्ट क्षेत्र वह है जो त्रिभुज, वृत्त और आयत अर्थात 5 में उभयनिष्ठ है।

II. कौन सी संख्या उन कलाकारों को दर्शाती है जो केवल खिलाड़ी भी हैं?

(a) 4

(b) 6

(c) 7

(d) 8

Ans. (b)

Sol. आवश्यक क्षेत्र वह है जो आयत और वृत्त में उभयनिष्ठ है लेकिन त्रिभुज के बाहर अर्थात 6 पर स्थित है।

III. कौन सी संख्या उन कलाकारों को दर्शाती है जो न तो खिलाड़ी हैं और न ही डॉक्टर हैं?

(a) 1

(b) 2

(c) 3

(d) 4

Ans. (a)

Sol. अभीष्ट क्षेत्र वह है जो आयत के अंदर है लेकिन वृत्त और त्रिभुज के बाहर अर्थात 1 है।

Sharing is caring!